本文摘要:摘要:HJM 模型的主要方法是,即在n个因子风险模型下,可以通过一个无风险资产和n个风险资产的组合构造资产市场上的所有资产,在HJM框架下,利用鞅方法等随机分析工具,考虑了与债券期货价格相关联的回望型外汇重置期权的定价问题,并得到了此类期权的定价公式
摘要:HJM 模型的主要方法是,即在n个因子风险模型下,可以通过一个无风险资产和n个风险资产的组合构造资产市场上的所有资产,在HJM框架下,利用鞅方法等随机分析工具,考虑了与债券期货价格相关联的回望型外汇重置期权的定价问题,并得到了此类期权的定价公式。
关键词:框架,外汇期权,重置期权,HJM 模型 高级会计师论文发表
1市场模型及预备知识
考虑一个连续交易的的完全金融市场,交易时间为
。在概率空间
中,W为概率空间上d维标准布朗运动.在上述概率空间中,HJM框架下的远期利率模型为:
汇率过程所满足的微分方程为:
其中k
{d,f}(d代表本国,f代表外国),
为k国的远期利率,
和
为取值于R的有界函数,
和
为取值于
的有界函数,“
”代表
上的欧氏内积,
为t时刻的汇率,表示一单位的外国货币可以转化为
单位的本国货币。
定义U时刻到期的k国零息票债券在t时刻的价格为:
单位的k国货币的银行存款在t时刻的价值为
,其中
为t时刻k国的即期利率。以k国货币计价,U时刻到期,T时刻交割的零息票债券的远期价格和期货价格分别记为
和
,且
则由
引理可得:
其中
,
引理
:以k国货币计价的零息票债券的价格
在k国测度
下满足微分方程:
0(3)
在本国概率测度
下,汇率过程满足的微分方程为:
(4)
对任意关于
可测的随机变量X,在本国概率测度
和外国概率测度
下有如下关系:
(5)
一单位零息票债券的远期价格
和期货价格
满足如下关系:
(6)
引理
0:在概率空间
中,对于任意时刻t
,当Random-Nikodym导数满足如下法则:
(7)
时,就称与本国概率测度
等价的新概率测度
为远期鞅测度.
引理
:任意X和Y,设
为它们的均值,
为它们的方差,则X的概率分布为:
(8)
2新型外汇重置期权定价
与债券期货价格相关联的外汇重置看涨期权在到期日时刻的收益可以分别表示为:
其中敲定汇率
和障碍价格
以本国货币计价,
定理1:定零息票债券的到期日为U,期货合同的交割日期和该期货期权的的执行日均为T,则与债券期货价格相关联的回望型外汇重置看涨期权在时刻t=0时的定价公式为:

证明:由引理1的(5)可得:
则引理
的(9)则可变为:
所以:
令
,由Girsanov定理可知存在如下关系:
由引理2可知:
所以

由(6)式和
可得
由(4),(5),(7)和
引理可得:
所以
+
所以
+
(15)
令
把(15)代入
,把(14)代入
,可推出:
由Girsanov定理可知:
在新的鞅测度
和
下
就就变形为:
令、
为了以后的计算方便,现定义以下记号:
;
当t=0时,由引理3可计算出计算
:
同理可算出
和
的值:
在零时刻,我们现在计算
的值
=
=
由引理3可知:
令
,密度函数
=
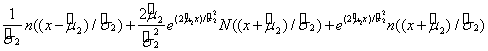
经计算可得:
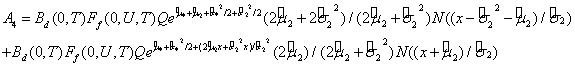
把
带入到V中,即可得到定理1的结果。
参考文献
1 Reiner E,Quanto mechanics[J],Risk,1992,5(3).59~63
2 Musiela M,Rutkowski M. Martingale Methods in Financial Modelling [M],
3 Steven Shreve.Stochastic Calculus and Finance [M].Carnegie Mellon University.
4 Chen Songnan. Financial Engineering [M]Shanghai : FuDan University Pubilishing Company ,2002, 187~204,303~311.
小编推荐优秀经济期刊 经济类期刊《中国周刊》征稿
《中国周刊》推崇独家的报道、独到的视野、独立的观点和独特的报道风格,强调原创性、权威性和可读性。坚持国家利益至上原则,记录变革的中国社会,鼓励和推动社会各领域的创新行为,关注和体察社会各阶层的生存状态,观察和分析社会各层面的流变异动,成为社会各界人士了解中国的最佳读本。
转载请注明来自发表学术论文网:http://www.fbxslw.com/jjlw/2133.html